CLAM::StatsTmpl< abs, T, U, initOrder > Class Template Reference

Class to hold basic statistics related to an array of arbitrary data. More...

#include <Stats.hxx>

List of all members.

Public Member Functions

 StatsTmpl (const Array< T > *data)
 ~StatsTmpl ()
void SetArray (const Array< T > *data)
 Method to change data array and reset all previous computations.
template<int order>
U GetMoment (const O< order > *)
 Get order-th raw moment.
template<int order>
void GetMoments (Array< U > &moments, const O< order > *)
 Get all raw moments up to the order indicated.
template<int order>
U GetCentralMoment (const O< order > *)
 Get order-th central moment.
template<int order>
void GetCentralMoments (Array< U > &centralMoments, const O< order > *)
 Get all central moments up to the order indicated.
template<int order>
U GetCenterOfGravity (const O< order > *)
 Get order-th center of gravity.
template<int order>
void GetCenterOfGravities (Array< U > &centerOfGravities, const O< order > *)
 Get all center of gravities up to the order indicated.
U GetMean ()
 Get mean, compute it if necessary.
U GetCentroid ()
 Get centroid, compute it if necessary.
U GetSpread ()
 Computes and returns the Spread arround the Centroid.
U GetStandardDeviation ()
 Get standard deviation, compute it if necessary.
U GetSkew ()
 Get skewness coefficient, compute it if necessary.
U GetKurtosis ()
 Get kurtosis, compute it if necessary.
U GetVariance ()
 Get variance, compute it if necessary.
T GetEnergy ()
 Get energy, compute it if necessary.
U GetGeometricMean ()
 Get the Geometric mean, and computes it if necessary.
T GetRMS ()
 Get the root means square (RMS), compute it if necessary.
T GetMax ()
 Get maximum value.
T GetMin ()
 Get minimum value.
U GetSlope ()
 Computes and returns the Slope.
U GetFlatness ()
 Get flatness, compute it if necessary.
void Reset ()
 Reset all the cached computations.

Detailed Description

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
class CLAM::StatsTmpl< abs, T, U, initOrder >

Class to hold basic statistics related to an array of arbitrary data.

Statistics are computed efficiently and reusing computations whenever possible.

Parameters:
abs whether the statistics are performed directly on the values (by default or template parameter=false) or on the absolute value of the array elements
T the array type
U the type of the resulting statistics
Precondition:
Most stats are not tolerant to size 0 data sets

Definition at line 86 of file Stats.hxx.

Constructor & Destructor Documentation

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
CLAM::StatsTmpl< abs, T, U, initOrder >::StatsTmpl ( const Array< T > *  data  )  [inline]

Definition at line 94 of file Stats.hxx.

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
CLAM::StatsTmpl< abs, T, U, initOrder >::~StatsTmpl (  )  [inline]

Definition at line 111 of file Stats.hxx.

Member Function Documentation

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
template<int order>
void CLAM::StatsTmpl< abs, T, U, initOrder >::GetCenterOfGravities ( Array< U > &  centerOfGravities,
const O< order > *   
) [inline]

Get all center of gravities up to the order indicated.

Definition at line 193 of file Stats.hxx.

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
template<int order>
U CLAM::StatsTmpl< abs, T, U, initOrder >::GetCenterOfGravity ( const O< order > *   )  [inline]

Get order-th center of gravity.

This method just acts as a selector, if order is greater than init order, we cannot assure that the pointer has been initialized and we need extra checks (slow downs).

Definition at line 187 of file Stats.hxx.

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
template<int order>
U CLAM::StatsTmpl< abs, T, U, initOrder >::GetCentralMoment ( const O< order > *   )  [inline]

Get order-th central moment.

This method just acts as a selector, if order is greater than init order, we cannot assure that the pointer has been initialized and we need extra checks (slow downs).

Definition at line 163 of file Stats.hxx.

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
template<int order>
void CLAM::StatsTmpl< abs, T, U, initOrder >::GetCentralMoments ( Array< U > &  centralMoments,
const O< order > *   
) [inline]

Get all central moments up to the order indicated.

Definition at line 169 of file Stats.hxx.

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
U CLAM::StatsTmpl< abs, T, U, initOrder >::GetCentroid (  )  [inline]

Get centroid, compute it if necessary.

The centroid of a function returns the position 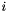$i$ around which most higher values are concentrated.

\[ Centroid(X) = \frac {\sum i \cdot x_i } {\sum x_i} \]

whenever the Mean(X) is less than 1e-7, then it will return the mid position

\[ \frac{Size(X)-1}{2} \]

Definition at line 238 of file Stats.hxx.

Referenced by CLAM::SpectralDescriptors::ConcreteCompute().

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
T CLAM::StatsTmpl< abs, T, U, initOrder >::GetEnergy (  )  [inline]

Get energy, compute it if necessary.

\[ Energy(X) = \sum{{x_i}^2 } \]

Definition at line 408 of file Stats.hxx.

Referenced by CLAM::SpectralDescriptors::ComputeLowFreqEnergyRelation(), CLAM::SpectralDescriptors::ComputeRolloff(), and CLAM::SpectralDescriptors::ConcreteCompute().

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
U CLAM::StatsTmpl< abs, T, U, initOrder >::GetFlatness (  )  [inline]

Get flatness, compute it if necessary.

The flatness is the relation among the geometric mean and the arithmetic mean.

\[ Flatness(X) = \frac {GeometricMean(X)} {Mean(X)} \]

Singularities and solution:

  • When the mean is lower than 1e-20, it is set at 1e-20
  • When the geometric mean is lower than 1e-20, it is set at 1e-20
    Todo:
    Explain why this is a mesure of the flatness
    Bug:
    Singularity solution don't work for non absolute stats

Definition at line 549 of file Stats.hxx.

Referenced by CLAM::SpectralDescriptors::ComputeSpectralFlatness().

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
U CLAM::StatsTmpl< abs, T, U, initOrder >::GetGeometricMean (  )  [inline]

Get the Geometric mean, and computes it if necessary.

The Geometric mean gives the mean magnitude order. It converges with the mean when all the values 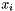$x_i$ are closer.

\[ GeometricMean(X) = {\left( \prod x_i \right)} ^ \frac{1}{Size(X) } \]

In order to make the computation cheap, For easy computation, logarithms are used.

\[ \log (GeometricMean(X)) = \frac { \sum \log_e x_i } { Size(X) } \]

Definition at line 430 of file Stats.hxx.

Referenced by CLAM::SpectralDescriptors::ConcreteCompute().

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
U CLAM::StatsTmpl< abs, T, U, initOrder >::GetKurtosis (  )  [inline]

Get kurtosis, compute it if necessary.

The Kurtosis of a distribution gives an idea of the degree of pickness of the distribution.

\[ Kurtosis(X) = \frac {\sum{\left( (x_i-Mean(X))^4\right)} } {\left( \sum{\left( x_i-Mean(X) \right)^2} \right) ^2 } \]

Tipical values:

  • A normal distribution of 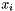$x_i$ values has a kurtosis near to 3.
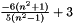
  • A constant distribution has a kurtosis of $\frac{-6(n^2+1)}{5(n^2-1)} + 3 $

Singularities and solutions:

  • Constant functions: Currently returns 3 althought it is not clear that it should be the right one, and it can vary on future implementations.

Definition at line 380 of file Stats.hxx.

Referenced by CLAM::SpectralDescriptors::ConcreteCompute().

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
T CLAM::StatsTmpl< abs, T, U, initOrder >::GetMax (  )  [inline]

Get maximum value.

Definition at line 448 of file Stats.hxx.

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
U CLAM::StatsTmpl< abs, T, U, initOrder >::GetMean (  )  [inline]

Get mean, compute it if necessary.

\[ Mean(X) = \frac {\sum x_i} { Size(X) } \]

Definition at line 213 of file Stats.hxx.

Referenced by CLAM::SpectralPeakDescriptors::ConcreteCompute(), and CLAM::SpectralDescriptors::ConcreteCompute().

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
T CLAM::StatsTmpl< abs, T, U, initOrder >::GetMin (  )  [inline]

Get minimum value.

Definition at line 454 of file Stats.hxx.

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
template<int order>
U CLAM::StatsTmpl< abs, T, U, initOrder >::GetMoment ( const O< order > *   )  [inline]

Get order-th raw moment.

This method just acts as a selector, if order is greater than init order, we cannot assure that the pointer has been initialized and we need extra checks (slow downs).

Definition at line 140 of file Stats.hxx.

Referenced by CLAM::SpectralDescriptors::ConcreteCompute().

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
template<int order>
void CLAM::StatsTmpl< abs, T, U, initOrder >::GetMoments ( Array< U > &  moments,
const O< order > *   
) [inline]

Get all raw moments up to the order indicated.

Definition at line 146 of file Stats.hxx.

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
T CLAM::StatsTmpl< abs, T, U, initOrder >::GetRMS (  )  [inline]

Get the root means square (RMS), compute it if necessary.

\[ \sqrt { \sum{{x_i}^2 } } \]

Todo:
Is it a mean??

Definition at line 442 of file Stats.hxx.

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
U CLAM::StatsTmpl< abs, T, U, initOrder >::GetSkew (  )  [inline]

Get skewness coefficient, compute it if necessary.

The Skewness of a distribution gives an idea of the assimetry of the variance of the values.

\[ Skewness(X) = \frac {\sum{\left( (x_i-Mean(X))^3\right)} } {\left( \sum{\left( x_i-Mean(X) \right)^2} \right) ^\frac{3}{2} } \]

Tipical values:

  • This function returns greater positive values when there are more extreme values above the median than below.
  • Returns negative values when there are more extreme values below the median than above.
  • Returns zero when the distribution of the 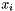$x_i$ values around the Median is equilibrated.

Singularities and solutions:

  • Constant functions: Currently returns NaN but, in the future, it should return 0 because it can be considered an equilibrated function.
Todo:
Give an order of magnitude, limits or something

Definition at line 352 of file Stats.hxx.

Referenced by CLAM::SpectralDescriptors::ConcreteCompute().

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
U CLAM::StatsTmpl< abs, T, U, initOrder >::GetSlope (  )  [inline]

Computes and returns the Slope.

The slope gives an idea of the mean pendent on the array:

  • Less than zero means that is decreasing
  • More than zero means that is increasing
  • Zero means that any tendency is the dominant

The Slope is defined as:

\[ {1 \over \sum{x_i}} { N \sum{i x_i } - \sum{i} \sum{x_i} \over {N \sum{i^2} - (\sum{i})^2 }} \]

We can transform this formula into one depending on the Centroid which is already calculated in order to obtain other stats:

\[ 6 { { 2 Centroid - N + 1} \over { N (N-1) (N+1)} } \]

The slope is relative to the array position index. If you want to give to the array position a dimentional meaning, (p.e. frequency or time) then you should divide by the gap between array positions. for example GetSlope/BinFreq for a FFT or GetSlope*SampleRate for an audio

Definition at line 492 of file Stats.hxx.

Referenced by CLAM::SpectralDescriptors::ConcreteCompute().

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
U CLAM::StatsTmpl< abs, T, U, initOrder >::GetSpread (  )  [inline]

Computes and returns the Spread arround the Centroid.

\[ Spread(Y) = \frac {\sum_{i=0}^{N-1}{(Centroid(Y)-x_i)^2 y_i} } { \sum_{i=0}^{N-1}{y_i} } \]

The spread gives an idea on how much the distribution is NOT concentrated over the distribution centroid. Taking the array as a distribution and the values being probabilities, the spread would be the variance of such distribution.

Significant values:

  • For a full concentration on a single bin: 0.0
  • For two balanced diracs on the extreme bins

    \[ Spread(BalancedDiracsDistribution) = {N^2 \over 4} \]

  • For a uniform distribution the spread it's:

    \[ Spread(UniformDistribution) = \frac{(N-1)(N+1)}{12} \]

Singularities and solution:

  • When 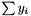$\sum{y_i}$ is less than 1e-14 it return the uniform distribution formula above.
  • Centroid NaN silence NaN is solved inside GetCentroid
  • When Centroid is less than 0.2, 0.2 is taken as the centroid value.

Normalization: Multiply the result by the square of the gap between arrays positions. ex. in an array representing a spectrum multiply by 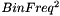$ BinFreq^2 $

Todo:

still not tested as stats but tested its usage for SpectralSpread

should use other stats than centroid to save computations

See also:
GetCentroid

Definition at line 295 of file Stats.hxx.

Referenced by CLAM::SpectralDescriptors::ConcreteCompute().

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
U CLAM::StatsTmpl< abs, T, U, initOrder >::GetStandardDeviation (  )  [inline]

Get standard deviation, compute it if necessary.

Definition at line 318 of file Stats.hxx.

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
U CLAM::StatsTmpl< abs, T, U, initOrder >::GetVariance (  )  [inline]

Get variance, compute it if necessary.

The variance is the mean cuadratic distance from the mean.

\[ Variance(X) = \frac {\sum{\left( (x_i-Mean(X))^2\right)} } {Size(X)} \]

Definition at line 395 of file Stats.hxx.

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
void CLAM::StatsTmpl< abs, T, U, initOrder >::Reset ( void   )  [inline]

Reset all the cached computations.

This method is called automatically if you change the data pointer using the SetData method, but it should be called explicitly whenever the values on that array changes externally.

Definition at line 564 of file Stats.hxx.

template<bool abs = false, class T = TData, class U = TData, int initOrder = 5>
void CLAM::StatsTmpl< abs, T, U, initOrder >::SetArray ( const Array< T > *  data  )  [inline]

Method to change data array and reset all previous computations.

Definition at line 128 of file Stats.hxx.

The documentation for this class was generated from the following file:
Generated by  doxygen 1.6.3